
・偏差値の「偏」は、かたよりを意味する漢字です。
・偏差値は、全体の平均からどのくらい離れているかを示す数値です。
・学力を相対的に評価する、ものさしの役割になります。
一例として、Aさんのテスト結果を見てみましょう。テストは5教科、各100点満点でした。
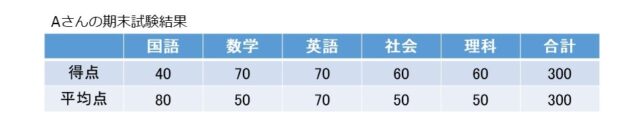
・合計点をみると、平均300点のところAさんも300点。ちょうど真ん中ですね。
・数学と英語が70点で他の教科よりもいい点数です。でも得点だけ見ずに、平均点と比較してみてください。
英語は、平均70点のところAさんも70点で、ちょうど真ん中です。
数学は、平均50点のところAさんは70点でした、みんな(平均)よりがんばった点数だったことが分かります。
・次に社会と理科を見ていきましょう。
この2教科は平均点も得点も、ともに同じなので、同じように評価されるかもしれません。
しかし、テストを受けた生徒全体のバラつき(偏り)があった場合にはどうでしょうか。
・例えば理科は、得手不得手の成績が出てしまい、0点から100点まで、各生徒の得点が分散していた(グラフでいうと、低い山で山裾が広い線形になった)。
・一方社会は、問題が易しかったのか全員得点が高く、50点を中心にギュッと集中していた(グラフでいうと、高い山で山裾も狭い線形になった)。
この場合、得点に差が出にくい社会のほうが「実は上位の成績だった」ということになります。
このように、平均点だけでは分からないバラつきかたを示すため、数値(標準偏差)を用いて平均値からの偏りを示した数値が「偏差値」です。
偏差値の計算式は

・例えば理科の標準偏差が20だったとすると、Aさんの社会の偏差値は55
・例えば社会の標準偏差が10だったとすると、Aさんの理科の偏差値は60
つまり、同じ得点、同じ平均点であったとしても、全体の「バラつき」によって偏差値に違いがでてくるわけです。
1. 得点が高ければ、偏差値も高くなる。
2. 得点が平均点と同じなら、偏差値は50になる。
3. 得点が「標準偏差」の分だけ上がると、偏差値は10上がる。
偏差値はおおむね75~25の間に収まります。
70~75が「非常に良い」、25~30だと「非常に悪い」と考えられます。
全体を見渡したとき、偏差値60以上は全体の15%、70以上となると2%程度となる場合が多くなります。
ちなみに標準偏差が分からない時、簡易版としての計算式は
(自分の得点ー平均点)÷2
この式でも導けますが、標準偏差を用いない簡易版のため、
だいたい±2ぐらい誤差がでてしまう式なので注意が必要です。目安として使いましょう。
「その2」へつづく
◆「偏差値ってなに?」「なぜ必要?」偏差値を理解して受験校選びを開始! その2
(よみうり進学メディア編集部)
☆よみうり進学メディアではX(旧Twitter)で記事更新をお知らせしています☆
X(旧Twitter)のフォローをすると、随時掲載情報が受け取れます。受験情報をお見逃しなく!
■よみうり進学メディアX(旧Twitter)はこちらをクリック
x.com@yag_ysmedia