都立高校の入試問題ってどんなもの？先輩たちが受けた試験問題を実際に見てみましょう。
「家庭教師のトライ」の先生による、解答付きです。
『都立高「数学」の全体傾向と対策』『数学の勉強法』もあります。
試しにチャレンジ、今は正解でなくても大丈夫です。
「都立高校の学力検査問題」のイメージをつかみ、今後の勉強に生かしていきましょう。
■都立高校の入試問題と解答・採点表（全教科）はこちらから：よみうり進学メディア
〈2025年度入試〉東京都 ２０２５年度 都立高校入学者選抜「学力検査問題」-令和7年度
【全体的な傾向】＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
問題の量や形式は例年通りでした。
前年度と比べると標準～応用レベルの問題が増えて、やや難しくなったと言えます。
ただ、全般的には基礎～標準レベルの問題が多く、まずはこのレベルの問題を確実に解けるようにしておくことが重要です。
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
【大問1】
小問集合（小問9 題・46 点）〔基本〕
問１～問7 は基本的な計算問題、問8 は確率の問題、問9 は作図問題でした。
これらはすべて教科書でも見かけるような基本問題で、授業をしっかり理解していれば解ける内容です。
ただ、問７の２次関数の変域に関する問題は解答ミスをしやすいため、注意が必要でした。
【大問2】 文字の利用・規則性（小問2 題・12 点）〔標準〕
例年通り「先生や生徒が問題を考えた」という想定で、円周上の点につけられた番号を使った計算問題と証明問題が出題されました。
問1 は、向かい合う数字の平均値と２乗の差の関係を求める問題です。
一見すると関係性がわかりにくいですが、具体的な数字で計算してみるとイメージしやすかったでしょう。
問2 は文字が４つも出てくる上に分数の計算が必要となるため、文字を減らして計算を工夫できるかがポイントでした。
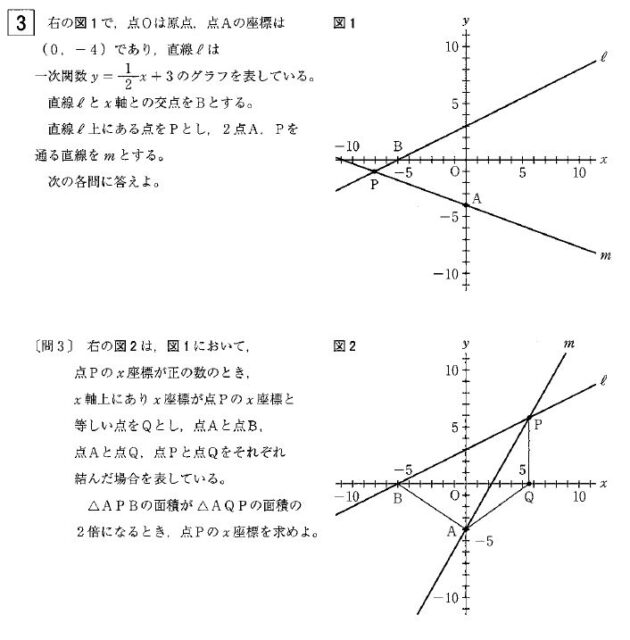
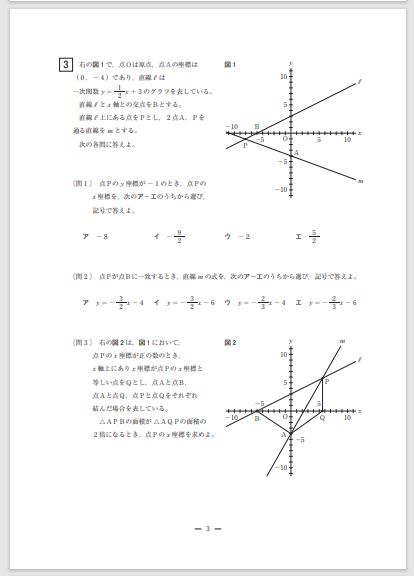【大問3】 1 次関数（小問3 題・15 点）〔標準〕
問1 は交点の座標を求める問題、問２は直線の式を求める問題、問３はグラフ中の2 つの三角形の面積の関係から座標を求める問題でした。
関数こそ異なりますが、昨年とよく似た問題設定であり、三角形の面積を求める問題の演習が十分できていれば比較的解きやすい問題でした。
【大問4】 平面図形（小問2 題・17 点）〔標準～応用〕
問1 は図形の性質を利用して角度を求める基本的な問題でした。
問２の①は、円周角の知識を使って正しく合同の証明を記述できるかが問われました。
問2 の②は面積の比を求める問題で、別の合同な三角形を見つけ出してその関係を活用する必要があり、図形問題への慣れが求められる難しい問題でした。
【大問5】 空間図形（小問2 題・10 点）〔標準〕
問1 は四角錐の体積を求める基本的な問題でした。
問2 は立体上の点を結んでできる三角形の面積を求める問題でした。三角形の高さを求めるための補助線さえ上手く引くことができれば、三平方の定理を活用して比較的簡単に解くことができました。
いずれも図形の性質を立体の中でうまく活用できるかが問われました。
【都立入試 「数学」の対策】＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
都立入試の数学では、中学で学習する範囲の様々な分野から出題されます。
最終的には３年生の知識が必要になることが多いですが、そこに至るまでの過程では１・２年生の知識を活用していく必要があります。
そのため、普段より苦手分野から目をそむけずに、基礎固めを行うことが肝心です。
また、大問1 の小問集合は安定した得点源になり得るため、そういう意味でも基礎固めを大切にしましょう。
さらに得点を伸ばすためには、完答が難しく本番でも差がつきやすい、証明や応用的な図形問題にトライすると良いでしょう。
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
都立高入試では中学３年間で学習する全範囲が出題範囲になりますので、今年度も各学年の学習内容から広く出題されました。
難易度としては教科書レベルの標準的な問題が多いため、まずはこれまで学んだ内容の復習をしっかりと行うことが大切です。
その上で新しい学習内容についても、基本をきちんと理解して自分の言葉で説明できるようにしましょう。
【計算問題】
計算力は、速さと正確さの2つの観点から考えることが重要です。都立高入試の数学では、特に正確さが求められます。
計算ミスを引き起こす主な原因には、「途中式を省略する」「似たような文字の見間違い」「検算を行わない」などがあります。
問題を解くときにこれらの点を意識して改善していくことで、より正確な計算能力が養われます。
【方程式・関数の問題】
方程式や関数の問題では、式を正しく立てることがカギとなります。問題文から適切に式を立てるためには、公式やその使い方をきちんと理解しておく必要があります。
新しく学ぶ内容に関しても、式をただ見るのではなく、その意味や使い方を確認しながら学ぶことが大切です。
関数の問題では、特に座標平面でのグラフと図形の関係が出題されやすいため、図形に注意しながら解いていく練習を積んでおきましょう。
【図形の問題】
図形問題では図形の性質を活用して解くことが大切です。各図形の持つ性質を思い出し、それを図に書きこむ練習をしておくと良いでしょう。
また、補助線を引く必要がある問題が多く見られるのも特徴です。「補助線の引き方」を整理し、実際に手を動かして線を引く練習をしましょう。
立体問題では、切断面や展開図を活用して問題を平面にして解くことがポイントです。
【データの問題】
今年度はデータの問題はありませんでしたが、全国的に見てもデータは年々出題されやすくなっています。
データの問題を解くには、用語の意味を理解していることが前提となります。その上で、図表やグラフを通して得られる情報を、自分の言葉で説明できるようにする必要があります。
特に、箱ひげ図が出題されやすいため、その読み方や解釈の仕方を確実にマスターしておくことが重要です。
【応用問題】
応用問題に取り組むには、まずは基本を理解しておくことが前提になります。そこから、応用問題特有の思考法や視点を養うことを目指しましょう。
重要なのは、解き方を丸暗記するのではなく、学んだ考え方を自分のものにして、異なる問題にも応用できるようにすることです。
応用問題では決まったパターンが出るわけではないため、様々な問題に対応できるように基本から理解を深めることが大事です。
【勉強の進め方について】
日々の学習では、まずは基礎知識をつけることから始め、それを踏まえて教科書の章末問題に取り組んでみましょう。
そして、週末や長期休暇など余裕のある時には、苦手分野の見直しを行うことが重要です。数学においては、1・2年生で習った内容が3 年生まで繋がっているため、苦手分野があるとその後の学習に影響します。
復習を通じて苦手を克服し、受験に向けて基礎を固めるためにも、今から着実に取り組むことが大切です。
出題：東京都教育委員会 解説：家庭教師のトライ
（よみうり進学メディア編集部）
☆よみうり進学メディアではX（旧Twitter）で記事更新をお知らせしています☆
X（旧Twitter）のフォローをすると、随時掲載情報が受け取れます。受験情報をお見逃しなく！
■よみうり進学メディアX（旧Twitter）はこちらをクリック
ｘ.com@yag_ysmedia
